活用例
飛行機の翼の生む騒音の予測
航空機から発生する騒音は、航空宇宙産業の効率と環境に関わる問題です。 機体全体の騒音の中で重要なのは翼の騒音です。 これは、翼とその周囲に生じる乱流との相互作用によって発生します。 翼の挙動を理解し、騒音を抑制する設計を行うためには、性能最適化を行う必要があります。
この例で使用した騒音のデータセットは、NASAによって処理されたものです。 このデータセットは、無響風洞で行われた2次元および3次元の翼の空力および音響試験から得られたものです。 NASAのデータセットは、さまざまなサイズのNACA 0012の翼を、さまざまな風洞の速度と迎角で測定したものです。 翼の長さと観測者の位置は統一して実験を行っています。
リンク:
アプリケーションの選択
予測する変数は音圧レベルで、連続的です。 そのため、この例では近似モデルを利用します。
ここでの目標は、音圧レベルを翼の特徴と対気速度の関数としてモデル化することです。
データセットの設定
最初のステップは、近似モデルの情報源であるデータセットの準備です。 データセットは以下で構成されています。
- データソース
- 変数
- インスタンス
この例では、変数(列)の数は6、インスタンス(行)の数は1503となっています。 変数は以下の6つです。
入力
- 周波数[Hz]
- 迎角[deg]
- 翼弦長[m]
- 自由流速度[m/s]
- 吸引側変位厚さ[m]
ターゲット
- 音圧レベル[dB]
このデータセットをランダムに分割して、それぞれ60％、20％、20％のインスタンスを含む、訓練、検証、テストのサブセットを作成します。 具体的には、訓練用に753個、検証用に375個、テスト用に375個のインスタンスを使用しています。
すべてのデータセットの設定が完了したら、データの品質を確認するためにいくつかの分析を行います。
例えば、データの分布を計算することができます。次の図は、対象となる変数のヒストグラムを示しています。
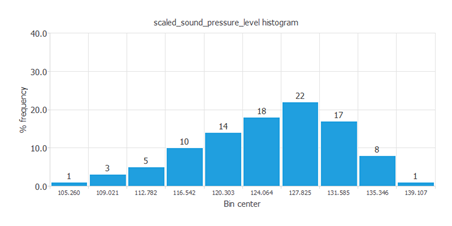上図のように、音圧レベルは正規分布に従っています。
次の図は、入力とターゲットの相関関係を表しています。
これにより、入力が音圧レベルに与える影響を確認することができます。
見ての通り、"frequency: 周波数"が音圧レベルに最も大きな影響を与えています。
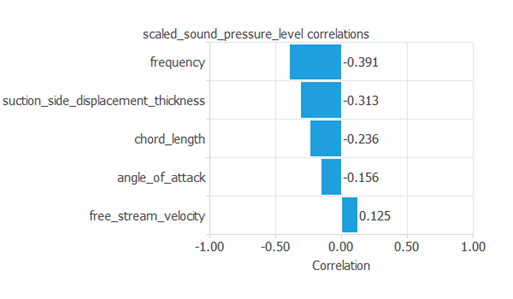
また、音圧レベルと周波数を比較した散布図を描くこともできます。
一般的に、周波数が高いほど音圧レベルは小さくなります。
ただし、音圧レベルは全ての入力に同時に依存します。
ネットワーク構造の設定
ニューラルネットワークは、周波数、迎角、翼弦長、自由流速度、吸込側変位厚さを入力とする関数として、音圧レベルを出力します。 近似モデルでは、ニューラルネットワークは次のように構成されています。
- スケーリング層
- パーセプトロン層
- アンスケーリング層
スケーリング層
スケーリング層は、元の入力値を正規化された値に変換します。 ここでは、入力値の平均値が0、標準偏差が1になるように、平均値と標準偏差のスケーリング手法が設定されています。
パーセプトロン層
ここでは、2つのパーセプトロン層がニューラルネットワークに挿入されています。 ほとんどの事例ではこの層の数で十分です。 第1層は5つの入力と3つのニューロンを持ち、第2層は3つの入力と1つのニューロンを持ちます。
アンスケーリング層
アンスケーリング層は、ニューラルネットワークから得られる正規化された値をターゲットに合わせて変換します。 ここでは、平均値と標準偏差のアンスケーリング手法を使用します。
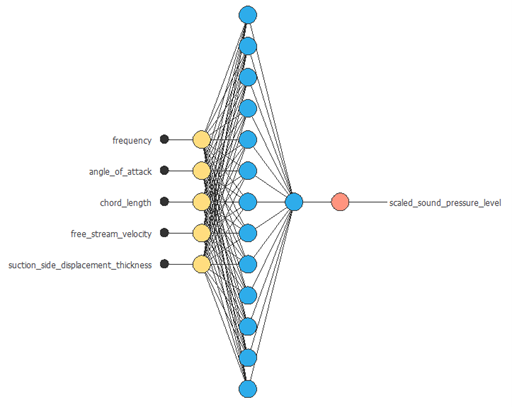
次の図は、ニューラルネットワークの構造を示しています。
このニューラルネットワークは、22個の調整可能なパラメータを持っています。
学習手法の設定
次のステップでは、ニューラルネットワークが何を学習するかを定義する学習手法を選択します。 一般的な学習手法は、2つのコンセプトで構成されています。
- 損失関数
- 最適化アルゴリズム
損失関数
損失関数として、L2正則化による正規化二乗誤差を選択しました。この損失関数は、近似モデルのデフォルトです。
最適化アルゴリズム
最適化アルゴリズムには、準ニュートン法を採用しました。 この最適化アルゴリズムは、今回のような中規模のアプリケーションではデフォルトとなっています。
学習手法の設定が完了したら、ニューラルネットワークに学習をさせます。
次の図は、学習過程において、エポック数(学習の繰り返し回数)に応じて訓練誤差(青)と検証誤差(オレンジ)が減少する様子を示しています。
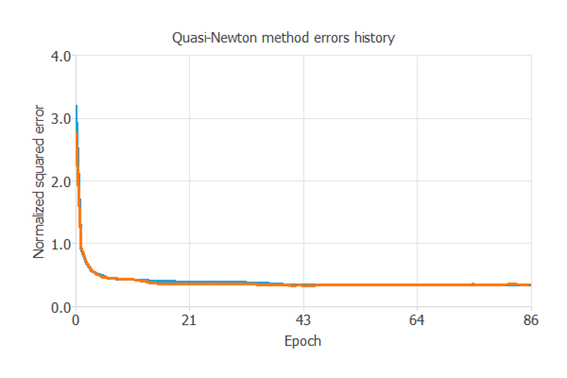トレーニングの結果で最も重要なのは、最終的な検証誤差です。
これがニューラルネットワークの汎化性能の指標となります。
ここでは、最終的な検証誤差は0.112NSEです。
モデル選択
モデル選択の目的は、最良の汎化性能を持つネットワーク構造を見つけることです。 つまり、先ほど得られた最終的な検証誤差(0.112NSE)の改善を目的とします。
最適な検証誤差は、入力とターゲットの関係を表すのに最も適した複雑さを持つモデルを使用することによって達成されます。
ニューロン数選択アルゴリズムは、このために最適なニューロン数を見つける役割を担います。
次のグラフは、ニューロン数選択アルゴリズムの結果を示しています。
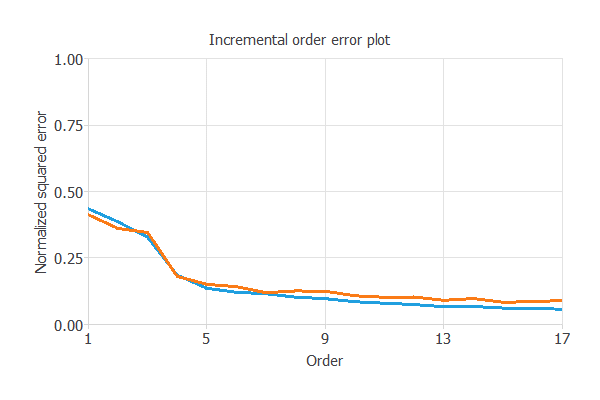青い線は、最終的な訓練誤差をニューロン数の関数としてプロットしています。
オレンジ色の線は、最終的な検証誤差をニューロン数の関数としてプロットしています。
このように、最終的な訓練誤差は、ニューロンの数が増えれば増えるほど常に減少します。
しかし、最終的な検証誤差は、ある時点で最小値をとります。
ここでは最適なニューロンの数は13であり、この時の検証誤差は0.100NSEになります。
次の図は、この例における最適なネットワーク構造を示しています。
テスト分析
テスト分析の目的は、学習したニューラルネットワークの汎化性能を検証することです。 そのために、ニューラルネットワークから得られた予測値を実測値と比較します。
近似モデルの標準的なテスト手法として、学習とは独立したテスト用インスタンスを用いた、予測値と実測値との間の線形回帰分析があります。
次の図は、このテスト分析によって得られた結果を示しています。
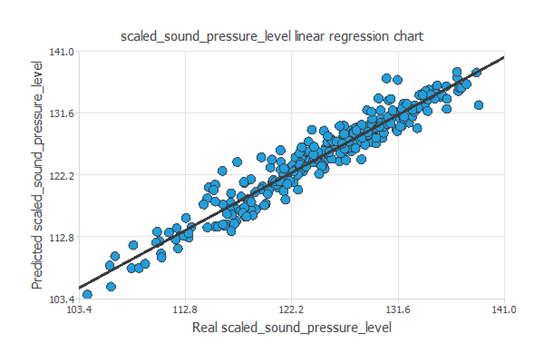上のグラフから、音圧レベルデータの全範囲をうまく予測できていることがわかります。
相関値はR2 = 0.952で、1に非常に近い値を示しています。
モデルの利用
このモデルは、学習時と同じデータ範囲で、新しい入力値を持つ翼の騒音を満足のいく品質で推定できるようになりました。
ニューラルネットワークのDirectional outputをプロットすることで、他のすべての入力値が固定されている場合に、ある入力値の変化に対して音圧レベルがどのように変化するかを見ることができます。
次のプロットは、周波数の関数としての音圧レベルを示しています。
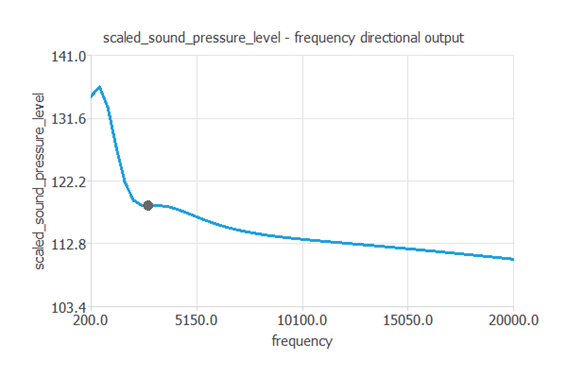周波数以外の入力値は次の値で固定しています。
- 迎角: 6.782 [deg]
- 翼弦長: 0.136 [m]
- 自由流速度: 50.860 [m/s]
- 吸引側変位厚さ: 0.011 [m]